Διαστάσεις

Ο σκοπός ενός σχεδίου είναι η παροχή των απαραίτητων πληροφοριών προκειμένου να είναι δυνατή η κατασκευή του σχεδιασμένου αντικειμένου σχεδίαση των απαραίτητων όψεων και τομών αποτελεί το πρώτο βήμα δημιουργίας ενός σχεδίου. Προκειμένου να θεωρηθεί ένα σχέδιο πλήρες, είναι απαραίτητο να καταγραφούν οι διαστάσεις του σχεδιαζόμενου τεμαχίου. Οι διαστάσεις τοποθετούνται πάνω στις όψεις του σχεδίου, αν είναι δυνατόν εκτός του περιγράμματος των όψεων, και δίνονται πάντα σε χιλιοστά [mm]. Ο τρόπος τοποθέτησης των διαστάσεων γίνεται με τέτοιο τρόπο ώστε το σχέδιο να είναι ευανάγνωστο και κατανοητό. Κάθε διάσταση τοποθετείται σε μία όψη. Η τοποθέτηση της ίδιας διάστασης σε παραπάνω από μία όψεις δεν επιτρέπεται. Επίσης, δεν επιτρέπεται η τοποθέτηση διαστάσεων που προκύπτουν από άλλες που έχουν ήδη αναγραφεί στο σχέδιο. Με τις διαστάσεις καθορίζονται οι αποστάσεις μεταξύ των ορατών γραμμών. Απαγορεύεται η τοποθέτηση διάστασης σε μη ορατή γραμμή. Αν είναι δυνατόν θα πρέπει οι διαστάσεις να ισοκατανέμονται στις όψεις του σχεδίου προκειμένου να υπάρχει ισορροπία. Ο τρόπος αναγραφής των διαστάσεων περιγράφεται πλήρως στο πρότυπο ISO 129.

• ΟΡΙΣΜΟΣ ΔΙΑΣΤΑΣΕΩΝ

Για την καταχώρηση διαστάσεων χρησιμοποιούνται δύο είδη γραμμών, η βοηθητική γραμμή και η γραμμή διάστασης, καθώς και δύο στοιχεία τα οποία είναι το σύμβολο οριοθέτησης της διάστασης και ο αριθμός διάστασης. Τα παραπάνω παρουσιάζονται στο Σχήμα 4.25.

Σχήμα 4.25: Ορισμός διαστάσεων.

Μια διάσταση ορίζεται σχεδιάζοντας δύο βοηθητικές γραμμές, τη γραμμή
διάστασης μαζί τα όρια και τον αριθμό της διάστασης. Η αρχή της
βοηθητικής γραμμής διάστασης βρίσκεται στο περίγραμμα του αντικειμένου
και το τέλος της επεκτείνεται 1mm – 2mm μετά τη γραμμή
διάστασης.
Σχεδιάζεται με λεπτή συνεχή γραμμή. Στο μεγαλύτερο ποσοστό των περιπτώσεων οι βοηθητικές γραμμές σχεδιάζονται κάθετα στο τμήμα του αντικειμένου που διαστασιολογείται. Η γραμμή διάστασης σχεδιάζεται μεταξύ των βοηθητικών γραμμών, επίσης με λεπτή συνεχή γραμμή. Η απόστασή της από το περίγραμμα ορίζεται στα 10mm, ενώ η απόσταση μεταξύ δύο διαδοχικών διαστάσεων ορίζεται στα 5mm – 7mm. Ο αριθμός της διάστασης τοποθετείται στο μέσο και πάνω από τη γραμμή διάστασης, όταν αυτή έχει οριζόντιο προσανατολισμό, ή αριστερά, όταν αυτή είναι κάθετη. Η συγκεκριμένη διάταξη ακολουθείται προκειμένου οι αριθμοί να διαβάζονται από αριστερά προς τα δεξιά και από κάτω προς τα πάνω. Το ύψος των αριθμών είναι συνήθως 3.5mm. Στα άκρα της γραμμής διάστασης τοποθετείται σύμβολο, το οποίο υποδηλώνει το όριο της διάστασης. Συνήθως το σύμβολο αυτό είναι ένα γεμάτο βέλος γωνίας 15° και μήκους 3.5mm (όταν χρησιμοποιείται η ομάδα γραμμών 0.7). Η σειρά σχεδίασης των παραπάνω στοιχείων είναι η εξής: βοηθητικές γραμμές, γραμμή διάστασης, όρια διάστασης και τέλος, αριθμός διάστασης.

Όπως φαίνεται στο Σχήμα 4.25, τόσο τα βέλη όσο και οι αριθμοί των διαστάσεων τοποθετούνται μεταξύ των βοηθητικών γραμμών. Υπάρχουν όμως περιπτώσεις όπου λόγω περιορισμένου χώρου είτε τα βέλη, είτε τα βέλη και ο αριθμός τοποθετούνται εκτός των βοηθητικών γραμμών, όπως απεικονίζεται στο Σχήμα 4.26. Κατά τη τοποθέτηση διαστάσεων, ειδικά σε συμμετρικά αντικείμενα, υπάρχει το ενδεχόμενο ο αριθμός της διάστασης να τέμνει κάποια αξονική γραμμή. Σε αυτήν την περίπτωση διακόπτεται η αξονική γραμμή προκειμένου να τοποθετηθεί ο αριθμός της διάστασης στο μέσο της γραμμής διάστασης, όπως παρουσιάζεται στο Σχήμα 4.27. Επίσης, πρέπει να αποφεύγεται η τομή των γραμμών διάστασης καθότι δυσχεραίνεται η ανάγνωση του σχεδίου. Σοβαρό λάθος είναι η καταχώρηση διαστάσεων σε μη ορατές ακμές. Στα Σχήματα 4.28, 4.29 και 4.30 δίδονται παραδείγματα λανθασμένης εφαρμογής διαστάσεων.

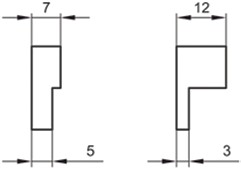
Σχήμα 4.26: Καταχώρηση διαστάσεων.

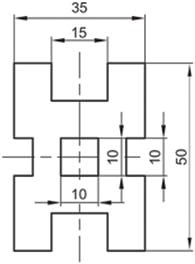
Σχήμα 4.27: Διακοπή αξονικών γραμμών κατά την καταχώρηση διαστάσεων.

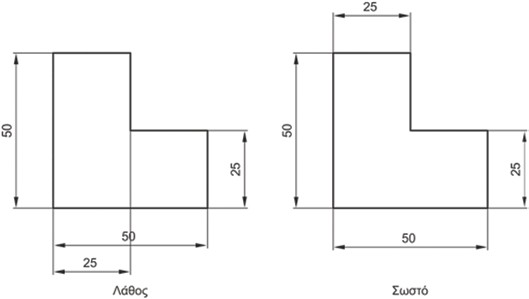
Σχήμα 4.28: Η τομή των γραμμών διαστάσεων πρέπει να αποφεύγεται.

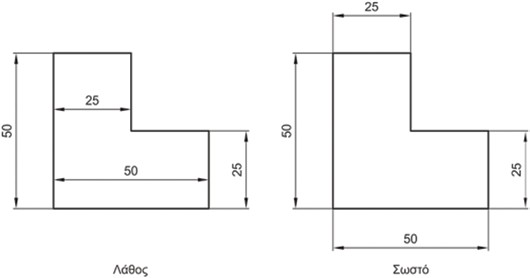
Σχήμα 4.29: Οι ορατές γραμμές δεν πρέπει να χρησιμοποιούνται ως βοηθητικές γραμμές διαστάσεων.

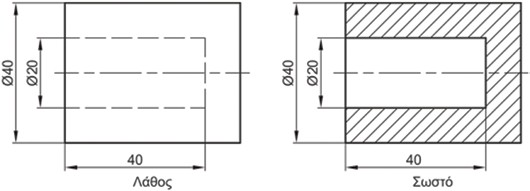
Σχήμα 4.30: Οι μη ορατές γραμμές δεν μπορούν να χρησιμοποιηθούν για την καταχώρηση διαστάσεων.

• ΤΟΠΟΘΕΤΗΣΗ ΔΙΑΣΤΑΣΕΩΝ

Η αναγραφή των διαστάσεων χρησιμοποιώντας γράμματα, αριθμούς και σύμβολα κατάλληλου ύψους αποσκοπεί στην βέλτιστη αναγνωσιμότητα του σχεδίου. Σε αυτήν την κατεύθυνση συμβάλει και η σωστή καταχώρηση των διαστάσεων, οι οποίες θα πρέπει να τοποθετούνται κατά τέτοιον τρόπο ώστε να μην διασταυρώνονται με κανέναν τρόπο με άλλα σχεδιαστικά αντικείμενα.

Οι διαστάσεις καταχωρούνται παράλληλα ως προς τις γραμμές διάστασης, στο μέσο της γραμμής διάστασης και πάνω από αυτή σε απόσταση 1mm, όπως φαίνεται στο Σχήμα 4.31a. Εξαίρεση από τον παραπάνω κανόνα αποτελούν περιπτώσεις όπου το κείμενο της διάστασης δεν χωράει μεταξύ των βοηθητικών γραμμών, στις οποίες η διάσταση μπορεί να καταχωρηθεί στην προέκταση της γραμμής διάστασης, όπως φαίνεται στο Σχήμα 4.26.

Η καταχώρηση των διαστάσεων πρέπει να γίνεται με τέτοιο τρόπο ώστε να διαβάζονται από αριστερά προς τα δεξιά και από κάτω προς τα πάνω. Σε πλάγιες διαστάσεις το κείμενο τοποθετείται όπως φαίνεται στο Σχήμα 4.31b. Διαστάσεις γωνιών καταχωρούνται όπως παρουσιάζεται στο Σχήμα 4.31c.

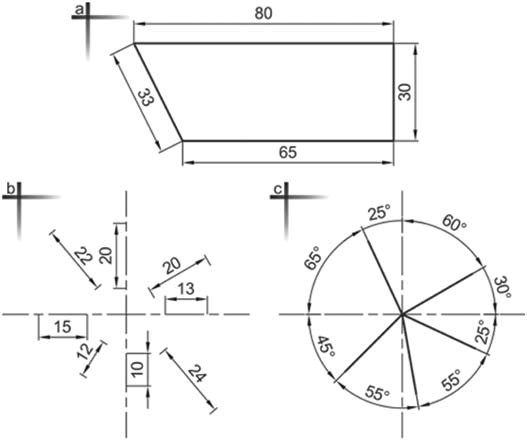
Σχήμα 4.31: Ορθή καταχώρηση γραμμικών και γωνιακών διαστάσεων.

Η τοποθέτηση των διαστάσεων στο μηχανολογικό σχέδιο συνήθως, πραγματοποιείται είτε βάσει ενός συστήματος αναφοράς ή επιπέδων αναφοράς, είτε σε σειρά σχηματίζοντας μια αλυσίδα, είτε, σε περιπτώσεις συμμετρικών αντικειμένων, γύρω από τον άξονα συμμετρίας.

Στο Σχήμα 4.32 παρουσιάζεται ο τρόπος τοποθέτησης διαστάσεων βάσει συστήματος αναφοράς. Οι άξονες αναφοράς (επισημασμένοι με κόκκινο χρώμα) καθορίζονται από τις ακμές του αντικειμένου που συναντώνται στην κάτω αριστερή γωνία. ΄Όλες οι διαστάσεις τοποθετούνται κατά τέτοιον τρόπο, ώστε η μία εκ των βοηθητικών γραμμών να είναι συγγραμμική με τους άξονες αναφοράς. Η θετική φορά μέτρησης ορίζεται από τα βέλη των αξόνων του σχήματος. Είναι δυνατή η διαστασιολόγηση του ίδιου αντικειμένου χρησιμοποιώντας δύο συστήματα αναφοράς για λόγους που έχουν να κάνουν με τη διευκόλυνση της διαδικασίας κατασκευής του αντικειμένου. Ένα αντίστοιχο παράδειγμα διαστασιολόγησης με δύο συστήματα αναφοράς δίδεται στο Σχήμα 4.33, όπου παρουσιάζεται το κατασκευαστικό σχέδιο μιας ατράκτου. Η διαδικασία μορφοποίησης της ατράκτου με χρήση εργαλειομηχανής (τόρνου), απαιτεί τη στήριξη και από τις δύο πλευρές με αποτέλεσμα να είναι απαραίτητο να καθοριστούν οι διαστάσεις με το σκεπτικό της κατασκευής. Κατ’ αυτήν την έννοια είναι σκόπιμο να τοποθετηθούν οι διαστάσεις βάσει δύο συστημάτων αναφοράς.

Σχήμα 4.32: Τοποθέτηση διαστάσεων βάσει συστήματος αναφοράς.

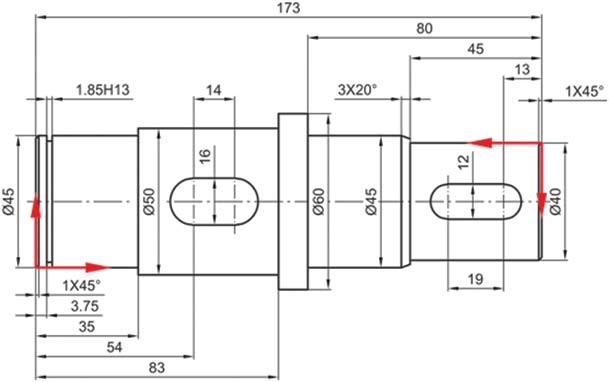
Σχήμα 4.33: Τοποθέτηση διαστάσεων βάσει δύο συστημάτων αναφοράς.

Η τοποθέτηση διαστάσεων σε σειρά παρουσιάζεται στο Σχήμα 4.34. Στη συγκεκριμένη περίπτωση οι διαστάσεις είναι συνεχόμενες σχηματίζοντας μια αλυσίδα. Οι διαστάσεις που τοποθετούνται στο ενδιάμεσο της αλυσίδας μοιράζονται τις βοηθητικές γραμμές τους με τις γειτονικές διαστάσεις.

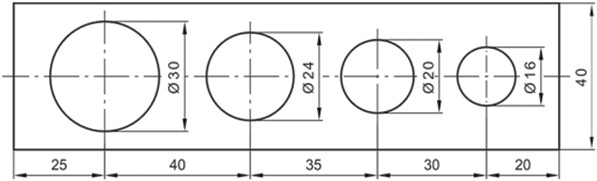
Σχήμα 4.34: Τοποθέτηση διαστάσεων σε σειρά.

Σε τεμάχια που παρουσιάζουν συμμετρία σε ένα ή και δύο επίπεδα, οι διαστάσεις τοποθετούνται γύρω από τους άξονες συμμετρίας, όπως παρουσιάζεται στο Σχήμα 4.35. Οι διαστάσεις τοποθετούνται στο κάτω και άνω μέρος του αντικειμένου και γύρω από τον άξονα συμμετρίας. Ωστόσο, στη συγκεκριμένη περίπτωση οι υπόλοιπες διαστάσεις του τεμαχίου, όπως φαίνεται στο αριστερό τμήμα της τομής, τοποθετούνται βάσει συστήματος αναφοράς. Διαπιστώνεται λοιπόν πως δεν απαγορεύεται ο συνδυασμός των διαφόρων μεθόδων τοποθέτησης διαστάσεων στην ίδια όψη.

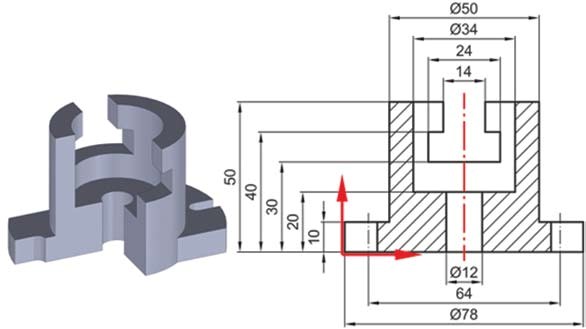
Σχήμα 4.35: Τοποθέτηση διαστάσεων σε συμμετρικά αντικείμενα.

• ΣΥΜΒΟΛΑ ΔΙΑΣΤΑΣΕΩΝ

Κατά την καταχώρηση διαστάσεων πολλές φορές γίνεται η χρήση ειδικών συμβόλων, προκειμένου να είναι ευκολότερη η κατανόηση της γεωμετρικής μορφής του αντικειμένου, στο οποίο καταχωρείται η διάσταση. Στον Πίνακα 4.2 αναφέρονται τα σύμβολα που χρησιμοποιούνται συνηθέστερα.

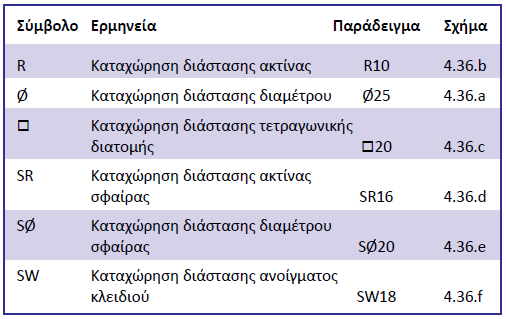
Πίνακας 4.2: Σύμβολα διαστάσεων

Στο Σχήμα 4.36 παρουσιάζονται παραδείγματα καταχώρησης συμβόλων διαστάσεων.

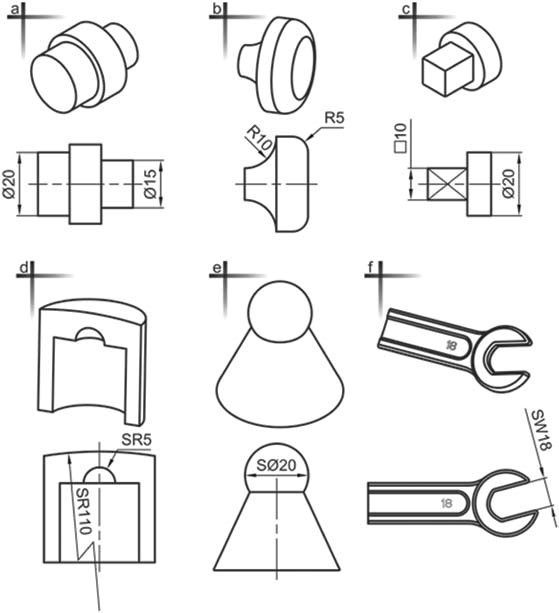
Σχήμα 4.36: Καταχώρηση συμβόλων διαστάσεων.

• ΕΙΔΗ ΔΙΑΣΤΑΣΕΩΝ

• Διαστάσεις Ακτίνων

Κατά την καταχώρηση διαστάσεων ακτίνων προτάσσεται πάντα το σύμβολο R πριν από τον αριθμό της διάστασης. Σε αυτήν την περίπτωση η γραμμή διάστασης έχει μόνο ένα όριο, το οποίο καταλήγει πάνω στην περιφέρεια του κύκλου, στην εξωτερική ή την εσωτερική μεριά της περιφέρειας. Το άλλο άκρο της γραμμής διάστασης καταλήγει στο κέντρο του κύκλου, το οποίο προσδιορίζεται ως η τομή δύο κάθετων αξονικών γραμμών. Ωστόσο, υπάρχουν περιπτώσεις όπου το κέντρο του κύκλου δε χρειάζεται να προσδιοριστεί. Σε αυτές τις περιπτώσεις η γραμμή διάστασης καταλήγει στο νοητό κέντρο του κύκλου. ΄Όταν ο χώρος είναι αρκετός, είναι προτιμότερο η διάσταση να τοποθετείται εντός του κύκλου. Στο Σχήμα 4.37 παρουσιάζονται παραδείγματα διαστασιολόγησης ακτίνων.

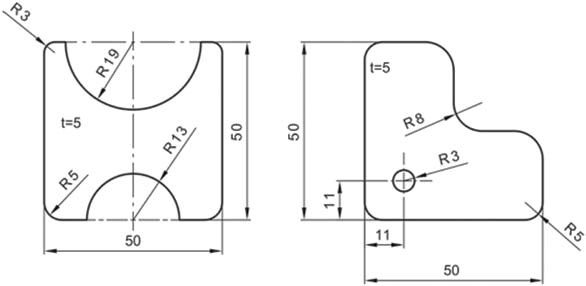
Σχήμα 4.37: Παραδείγματα καταχώρησης διαστάσεων ακτίνων.

• Διαστάσεις Διαμέτρων

Σε αντίθεση με τις διαστάσεις ακτίνων όπου το σύμβολο R συνοδεύει όλους τους αριθμούς των διαστάσεων, στις διαστάσεις διαμέτρων το σύμβολο Ø προτάσσεται του αριθμού διάστασης στις παρακάτω περιπτώσεις:

• Όταν από τη σχεδιασμένη όψη του αντικειμένου δεν προκύπτει ότι το στοιχείο που διαστασιολογείται είναι κύκλος, όπως φαίνεται στο Σχήμα 4.38a.
• Στην περίπτωση που η γραμμή διάστασης έχει μόνο ένα όριο (διάσταση Ø45 του Σχήματος 4.38b).
• Όταν καταχωρείται διάσταση διαμέτρου με ενδεικτική γραμμή (διάσταση Ø6 του Σχήματος 4.38b).

Αντίθετα, στις διαστάσεις 75 και 15 του Σχήματος 4.38b δε χρειάζεται να χρησιμοποιηθεί το σύμβολο Ø, καθότι από την όψη είναι ξεκάθαρο πως πρόκειται για κύκλους.

Όπως φαίνεται στις διαστάσεις των Σχημάτων 4.38a και b, αυτές δεν είναι ανάγκη να τοποθετηθούν στο μέσο της γραμμής διάστασης, αλλά μετατοπίζονται προς τα όρια της γραμμής διάστασης προκειμένου να μην τέμνονται από τις αξονικές γραμμές.



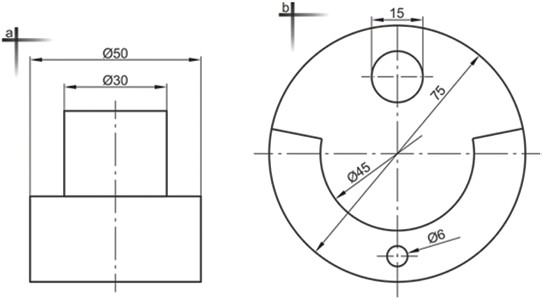
Σχήμα 4.38: Παραδείγματα καταχώρησης διαστάσεων διαμέτρων.

• Διαστάσεις Γωνίων

Για τη διαστασιολόγηση γωνιών οι βοηθητικές γραμμές τοποθετούνται κατά τέτοιον τρόπο ώστε να συγκλίνουν προς το κέντρο του τόξου. Οι γωνίες μπορούν να εκφραστούν σε μοίρες, όπου δίπλα στον αριθμό τοποθετείται το σύμβολο της μοίρας, ή, σε μοίρες, λεπτά και δευτερόλεπτα, τοποθετώντας σε αυτή την περίπτωση τα αντίστοιχα σύμβολα: μοίρα (°), λεπτά (‘), δευτερόλεπτα (“). Στο Σχήμα 4.39 παρουσιάζονται οι τρόποι διαστασιολόγησης γωνιών.



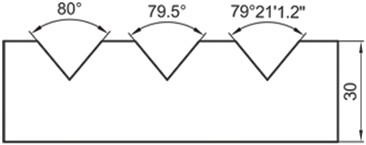
Σχήμα 4.39: Παραδείγματα καταχώρησης διαστάσεων γωνιών.

• Διαστάσεις σε Κλίσεις και Λεπτύνσεις

Στο Σχήμα 4.40 παρουσιάζεται ο τρόπος τοποθέτησης διαστάσεων σε κλίσεις και λεπτύνσεις. ΄Όπως φαίνεται και στο σχήμα η κλίση μιας ευθείας υπολογίζεται από το λόγο της διαφοράς των υψών των άκρων της ευθείας προς την απόστασή τους. Με αντίστοιχο τρόπο ορίζεται η λέπτυνση τεμαχίων τετραγωνικής διατομής, όπου η διατομή δεν παραμένει σταθερή κατά την έννοια του μήκους, αλλά μικραίνει, με αποτέλεσμα η αρχική και τελική τετραγωνική διατομή να έχουν διαφορετική διάσταση, αλλά το κέντρο τους να διέρχεται από τον ίδιο άξονα.



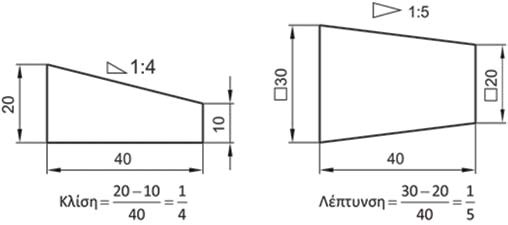
Σχήμα 4.40: Παραδείγματα καταχώρησης διαστάσεων κλίσεων και λεπτύνσεων.

Η ένδειξη της κατεύθυνσης της κλίσης γίνεται τοποθετώντας ένα μικρό ορθογώνιο τρίγωνο πριν από την τιμή της κλίσης. Αντίστοιχα, στη λέπτυνση χρησιμοποιείται ένα μικρό ισοσκελές τρίγωνο. Η τιμή της κλίσης ή της λέπτυνσης μπορεί να οριστεί και ως ποσοστό αντί για το λόγο του προηγούμενου σχήματος. Έτσι, αντί για ¼ μπορεί να εισαχθεί 25%.

• Διαστάσεις Σπειρωμάτων

Για τα συνήθη τυποποιημένα σπειρώματα είναι απαραίτητο να οριστούν η βασική διάσταση του σπειρώματος, η οποία προσδιορίζει την εξωτερική διάμετρο του σπειρώματος, προτάσσοντας κατά περίπτωση τα σύμβολα Μ, R, Tr (M = απλό μετρικό σπείρωμα, R = σφαιρικό σπείρωμα, Tr = τραπεζοειδές σπείρωμα), όπως αυτά καθορίζονται στο πρότυπο DIN 202 του 1988. Επίσης, είναι απαραίτητο να ορίζεται και το μήκος του σπειρώματος. Στο Σχήμα 4.41 δίνονται παραδείγματα καταχώρησης διαστάσεων σε σπειρώματα.



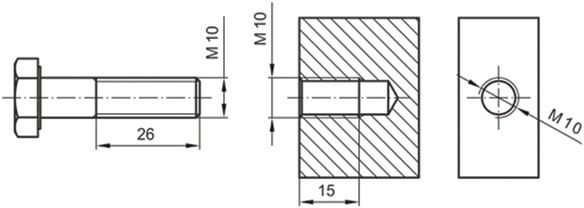
Σχήμα 4.41: Παραδείγματα καταχώρησης διαστάσεων σε σπειρώματα.

• Διαστάσεις σε Τόξα Κύκλου

Στην καταχώρηση διαστάσεων τόξων τοποθετείται πάνω από τη αριθμό της διάστασης ένα μικρό τόξο προκειμένου ώστε να επισημανθεί ότι πρόκειται για διάσταση που αναφέρεται σε μήκος τόξου κύκλου. Σε τόξα όπου η περιεχόμενη γωνία είναι μικρότερη από 90°, οι βοηθητικές γραμμές είναι παράλληλες με τη διχοτόμο της περιεχόμενης γωνίας, ενώ σε περίπτωση που η γωνία του τόξου υπερβαίνει τις 90°, τότε οι βοηθητικές γραμμές διάστασης έχουν κατεύθυνση προς το κέντρο του τόξου, όπως παρουσιάζεται στο Σχήμα 4.42.



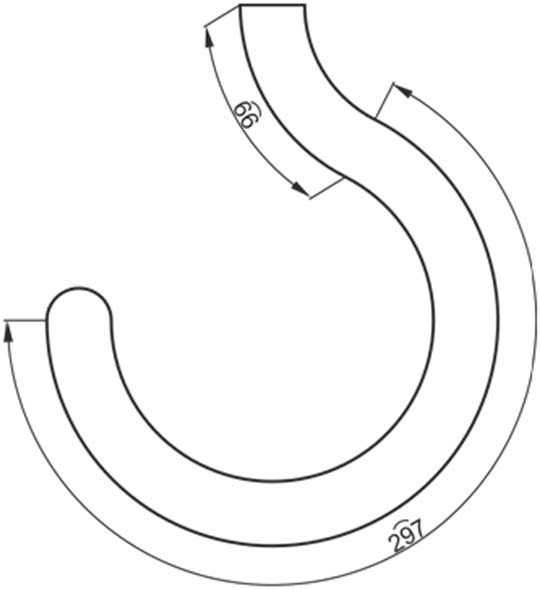
Σχήμα 4.42: Τοποθέτηση διαστάσεων σε τόξα κύκλου.