- ΣΠΕΙΡΩΜΑΤΑ – ΚΟΧΛΙΕΣ
- Είδη σπειρωμάτων
- Είδη κοχλιών και περικοχλίων
- Σχεδίαση σπειρωμάτων & κοχλιών
Στη μηχανολογική σχεδίαση χρησιμοποιούνται πολλά τεμάχια, τα οποία επιτελούν συγκεκριμένες λειτουργίες. Παραδείγματα αποτελούν οι κοχλίες, οι πήροι, οι σφήνες, τα έδρανα κύλισης και ολίσθησης, κ.α. Προκειμένου να είναι ευκολότερη και απροβλημάτιστη η διασύνδεση σχεδίου – κατασκευής τα συγκεκριμένα τεμάχια έχουν τυποποιηθεί σύμφωνα με κανονισμούς DIN και ISO. Στους συγκεκριμένους κανονισμούς περιγράφεται και ο τρόπος σχεδίασης των συγκεκριμένων αντικειμένων. Στις επόμενες παραγράφους παρουσιάζονται οι τρόποι απεικόνισης αυτών των τεμαχίων στο μηχανολογικό σχέδιο.
Οι κοχλίες είναι ένα από τα τεμάχια που χρησιμοποιούνται συχνότερα στις μηχανολογικές κατασκευές. Η χρήση τους επιτρέπει την εφαρμογή λυόμενων συνδέσεων με ιδιαίτερα χαμηλό κόστος, ταυτόχρονα όμως, αυτές οι συνδέσεις διαθέτουν υψηλή αξιοπιστία. Η βασική παράμετρος που έχει καταστήσει τους κοχλίες απαραίτητους είναι η επίτευξη υψηλού αξονικού φορτίου, εφαρμόζοντας μικρή σχετικά ροπή σύσφιξης, η οποία μπορεί να είναι και ελεγχόμενη. Το στοιχείο των κοχλιών στο οποίο μετατρέπεται η ροπή σύσφιξης σε αξονικό φορτίο, είναι το σπείρωμα, το οποίο μπορεί να διαμορφωθεί με την εφαρμογή διάφορων μεθοδολογιών, όπως η μορφοποίηση με πλαστική παραμόρφωση, η μορφοποίηση με αφαίρεση υλικού κ.α. Στο Σχήμα 4.43 παρουσιάζεται κοχλίας με κυλινδρική κεφαλή Allen, όπου σε λεπτομέρεια φαίνεται η μορφή του σπειρώματος του κοχλία.

Σχήμα 4.43: Κοχλίας με κυλινδρική κεφαλή Allen με λεπτομέρεια του σπειρώματος.
Ο πιο διάσημος κοχλίας που έχει καταγράψει η ιστορία, είναι ο κοχλίας του Αρχιμήδη (Σχήμα 4.44), ο οποίος χρησιμοποιείται ακόμη και στις μέρες μας για την άντληση και μεταφορά υγρών αλλά και υλικών σε μορφή μικρών κόκκων, από ένα χαμηλό επίπεδο σε ένα άλλο που βρίσκεται σε μεγαλύτερο ύψος.
Η γεωμετρία του σπειρώματος μπορεί να δημιουργηθεί εάν τυλιχθεί νήμα, το οποίο παρουσιάζει γωνία α σε σχέση με το οριζόντιο επίπεδο, γύρω από την επιφάνεια ενός κυλίνδρου. Με αυτή τη διαδικασία δημιουργείται μία ελίκωση, η οποία έχει την κλίση της ευθείας, διάμετρο αυτή του κυλίνδρου και βήμα p (η απόσταση που προκύπτει κατά τη μετατόπιση ενός σημείου της έλικας για μία περιστροφή ίση με 360°), όπως παρουσιάζεται στο Σχήμα 4.45. Η συγκεκριμένη έλικα αποτελεί τη βασική γεωμετρία ενός σπειρώματος, το οποίο επίσης χαρακτηρίζεται από την κλίση και το βήμα.
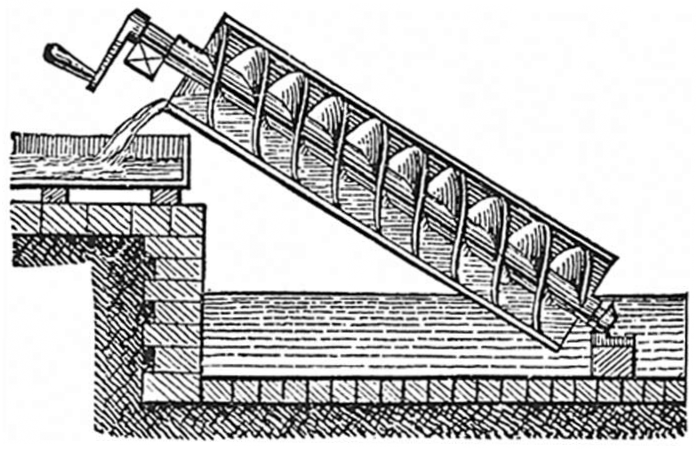
Σχήμα 4.44: Σχηματική αναπαράσταση του κοχλία του Αρχιμήδη.
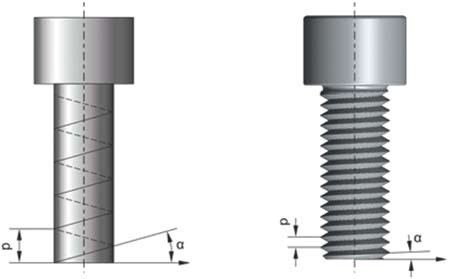
Σχήμα 4.45: Δημιουργία έλικας και αντιστοίχηση μεγεθών με ένα σπείρωμα.
Τα γεωμετρικά χαρακτηριστικά ενός σπειρώματος παρουσιάζονται στο Σχήμα 4.46 και είναι τα παρακάτω:
• Η εξωτερική διάμετρος d
• H μέση διάμετρο d2
• H διάμετρος ποδιού ή διάμετρος πυρήνα του κοχλία d3
• Το βάθος του σπειρώματος h3
• Το βήμα του σπειρώματος p
• Η γωνία κλίσης των παρειών του σπειρώματος β
Όπως προαναφέρθηκε, όλα τα παραπάνω μεγέθη είναι τυποποιημένα και οι διαστάσεις δίνονται από αντίστοιχους κανονισμούς. Παρακάτω θα παρουσιαστούν πίνακες στους οποίους δίνονται οι διαστάσεις των μεγεθών των σπειρωμάτων.

Σχήμα 4.46: Γεωμετρικά χαρακτηριστικά σπειρώματος.
Υπάρχουν πέντε διαφορετικές γεωμετρίες σπειρωμάτων, το τριγωνικό, το τραπεζοειδές, το ορθογωνικό, το πριονοειδές και το στρογγυλό (Σχήμα 4.47). Από τα παραπάνω, μόνο το τριγωνικό εφαρμόζεται σε κοχλίες και περικόχλια που προορίζονται για συνδέσεις, ενώ τα υπόλοιπα χρησιμοποιούνται σε κοχλίες κίνησης.

Σχήμα 4.47: Είδη σπειρωμάτων ανάλογα με τη γεωμετρία.
Ο κάθε τύπος σπειρώματος συμβολίζεται με διαφορετικό τρόπο. Έτσι, για το τριγωνικό μετρικό σπείρωμα χρησιμοποιείται το σύμβολο Μ, το τραπεζοειδές το σύμβολο Tr, και για το στρογγυλό το σύμβολο Rd. Παραδείγματα χρήσης των συμβόλων καθώς και η επεξήγησή τους δίνονται στον επόμενο πίνακα.

Πίνακας 4.3: Παραδείγματα χρήσης συμβόλων σπειρωμάτων.
Στο σχήμα του Πίνακα 4.4 παρουσιάζεται το μετρικό σπείρωμα κατά ISO, καθώς επίσης οι σχέσεις που συνδέουν τα διάφορα γεωμετρικά μεγέθη, στους οποίους τα μικρά γράμματα αναφέρονται στον κοχλία, ενώ τα κεφαλαία στο περικόχλιο. Το συγκεκριμένο σπείρωμα έχει δύο μορφές, το κανονικό και το λεπτό. Το λεπτό σπείρωμα χαρακτηρίζεται από μικρότερα βάθη σπειρώματος και μικρότερο βήμα, με αποτέλεσμα να προκύπτουν περισσότερες σπείρες ανά μήκος κοχλία και να αυξάνεται κατ’ αυτόν τον τρόπο η αντοχή του, σε βάρος όμως του κόστους. Στον Πίνακα 4.5 παρουσιάζονται οι διαστάσεις για το λεπτό μετρικό σπείρωμα.

Πίνακας 4.4: Μορφή κανονικού τριγωνικού μετρικού σπειρώματος και διαστάσεις σύμφωνα με το ISO – DIN 13-1.
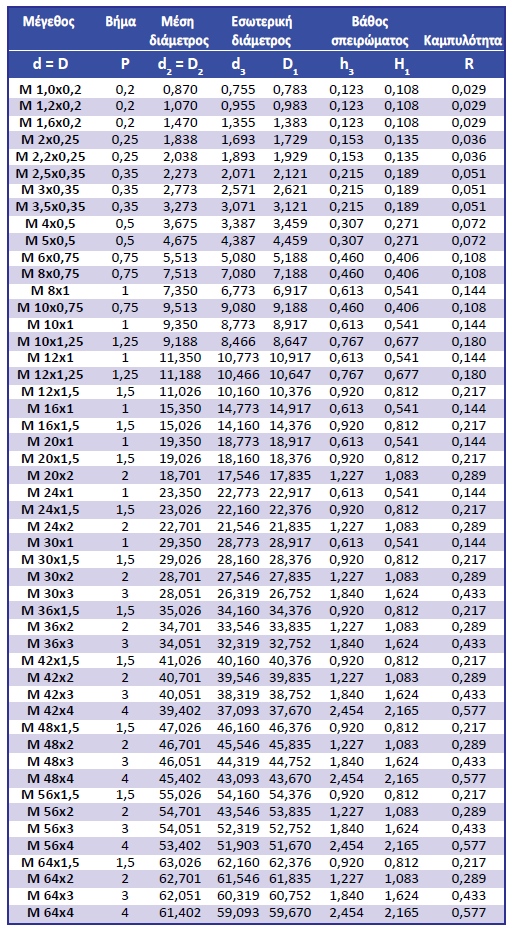
Πίνακας 4.5: Διαστάσεις λεπτού μετρικού σπειρώματος DIN 13-2.
Στον Πίνακα 4.6 δίνονται οι διαστάσεις για μετρικό τραπεζοειδές σπείρωμα κατά DIN 103. Το τραπεζοειδές σπείρωμα χρησιμοποιείται ως επί το πλείστον σε κοχλίες κίνησης.
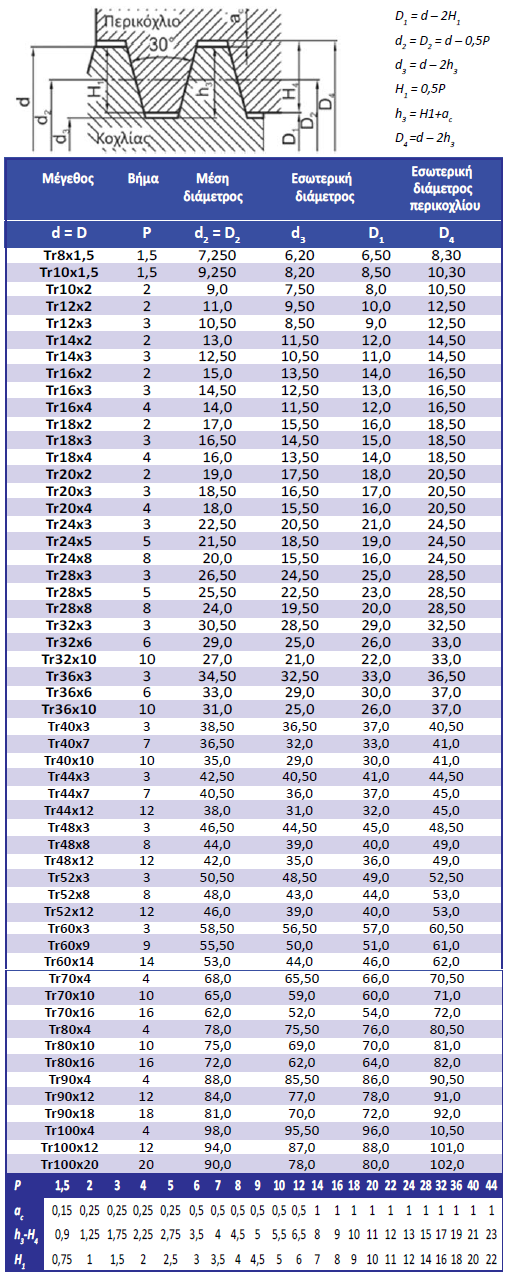
Πίνακας 4.6: Διαστάσεις μετρικού τραπεζοειδούς σπειρώματος κατά DIN 103.
Στον Πίνακα 4.7 δίνονται οι διαστάσεις για μετρικό στρογγυλό σπείρωμα κατά DIN405. Το στρογγυλό σπείρωμα χρησιμοποιείται σε κοχλίες κίνησης σε εφαρμογές όπου απαιτείται υψηλή ακρίβεια τοποθέτησης, σε πλαστικές και γυάλινες συσκευασίες καθώς και σε τεμάχια που έχουν ιατρική χρήση.
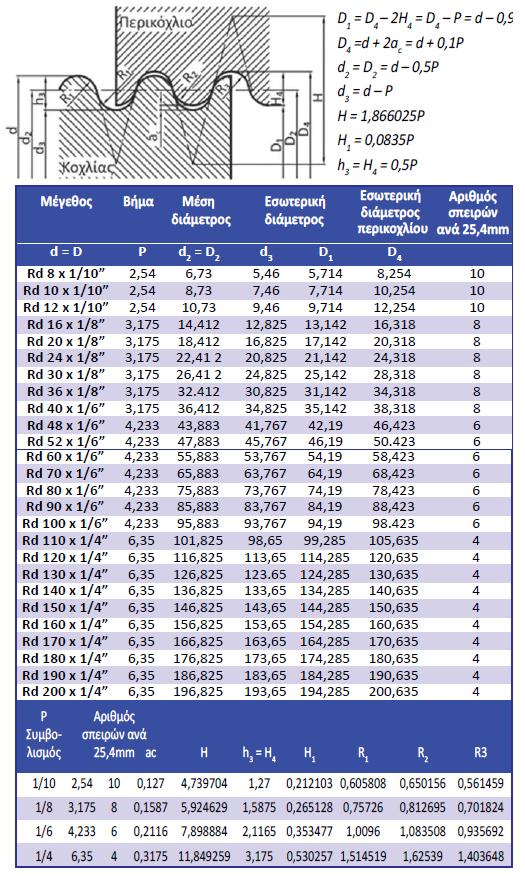
Πίνακας 4.7: Διαστάσεις μετρικού στρογγυλού σπειρώματος κατά DIN405.
Οι κοχλίες και τα περικόχλια είναι τεμάχια με τη συχνότερη χρήση σε διάφορες κατασκευές. ΄Έχουν υψηλή αντοχή και γι’ αυτόν το λόγο μορφοποιούνται από χαλύβδινο σύρμα με συνδυασμό πλαστικής παραμόρφωσης και διέλασης. Κατασκευάζονται με διάφορες παραλλαγές της μορφής τους, κυρίως όμως όσο αφορά το τμήμα της κεφαλής και του σπειρώματος.
Τα κύρια μέρη ενός κοχλία είναι η κεφαλή, ο κορμός και το σπείρωμα. Η κεφαλή ενός κοχλία μπορεί να έχει μορφή εξαγωνική, κυλινδρική, φραιζάτη, φακοειδή ή ακόμη και να μην υφίσταται (κοχλίες χωρίς κεφαλή). Για κάθε ονομαστική διάμετρο ενός κοχλία προκύπτουν διάφορα μήκη προκειμένου να ικανοποιούνται διάφορες περιπτώσεις συνδέσεων με κοχλίες. Στο Σχήμα 4.48 παρουσιάζονται διάφοροι τύποι κοχλιών και περικοχλίων.
Οι χαρακτηριστικές διαστάσεις ενός κοχλία παρουσιάζονται στο Σχήμα 4.49 και είναι η εξωτερική διάμετρος, και το ονομαστικό μήκος. ΄Άλλες διαστάσεις είναι το μήκος του σπειρώματος, το μήκος του κοχλία, το ύψος της κεφαλής και αναλόγως της περίπτωσης, η διάμετρος της κεφαλής, όταν πρόκειται για κυλινδρική κεφαλή, ή το άνοιγμα του κλειδιού, όταν πρόκειται για εξαγωνική κεφαλή.

Σχήμα 4.48: Διάφοροι τύποι κοχλιών και περικοχλίων.

Σχήμα 4.49: Χαρακτηριστικές διαστάσεις κοχλιών.
Στον Πίνακα 4.8 παρουσιάζονται συνήθεις κοχλίες, η απεικόνισή τους στο μηχανολογικό σχέδιο, καθώς και η τυποποίησή τους.
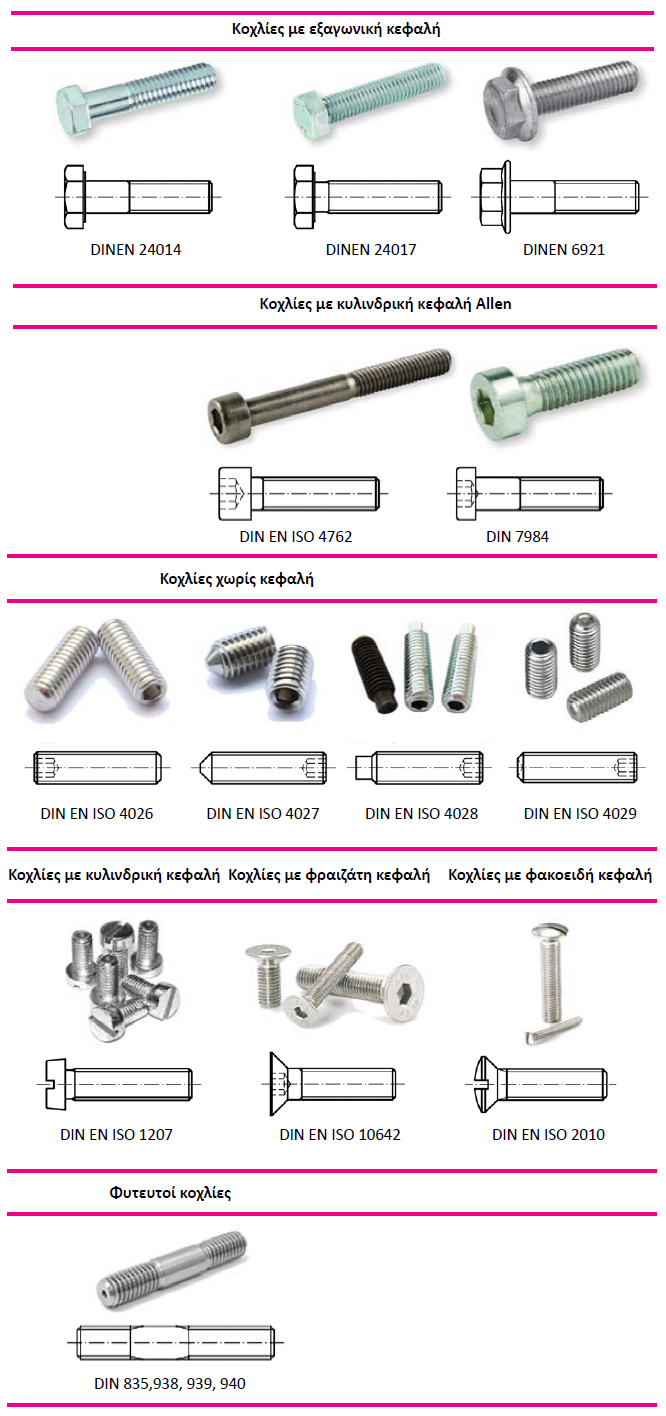
Πίνακας 4.8: Διάφοροι τύποι κοχλιών με τις τυποποιήσεις τους.
Στους Πίνακες 4.9 και 4.10 δίνονται οι διαστάσεις κοχλιών εξαγωνικής κεφαλής και κυλινδρικής κεφαλής Allen.

Πίνακας 4.9: Διαστάσεις κοχλιών εξαγωνικής κεφαλής κατά DIN 24014.

Πίνακας 4.10: Διαστάσεις κοχλιών με κυλινδρική κεφαλή Allen κατά DIN ΕΝ ISO 4762.
Τα περικόχλια είναι επίσης τυποποιημένα, σε αντιστοιχία με τους κοχλίες, κατασκευάζονται σε διάφορες μορφές, αναλόγως την εφαρμογή για την οποία προορίζονται. Στον Πίνακα 4.11 δίνονται οι διαστάσεις για τα συνηθέστερα περικόχλια.

Πίνακας 4.11: Διαστάσεις περικοχλίων.
Στο μηχανολογικό σχέδιο δε σχεδιάζεται η πραγματική μορφή του σπειρώματος, καθότι από τη μία είναι αρκετά περίπλοκη ενώ από την άλλη πρόκειται για γεωμετρία η οποία είναι τυποποιημένη, οπότε η σχεδίαση της πραγματικής γεωμετρίας δε δίνει περαιτέρω πληροφορίες. Για τους παραπάνω λόγους η σχεδίαση των σπειρωμάτων γίνεται συμβολικά. Σχεδιάζεται με δύο ευθείες, μία που διέρχεται από τις κορυφές του σπειρώματος με παχιά συνεχή γραμμή και η δεύτερη να διέρχεται από τη βάση του σπειρώματος. Αναλόγως το τεμάχιο στο οποίο σχεδιάζεται το σπείρωμα προκύπτουν επιπλέον σχεδιαστικές λεπτομέρειες οι οποίες θα επιδειχθούν στη συνέχεια.
Οι οπές που φέρουν σπείρωμα κατατάσσονται σε δύο κατηγορίες τις διαμπερείς, που η οπή διατρέχει όλο το τεμάχιο και τις τυφλές, στις οποίες η οπή τερματίζεται σε συγκεκριμένο βάθος. Και στις δύο περιπτώσεις, αρχικά, πραγματοποιείται η διάνοιξη της οπής με τρυπάνι μικρότερης διαμέτρου και στη συνέχεια, μορφοποιείται το σπείρωμα με κατάλληλο εργαλείο (σπειροτόμος). Στην περίπτωση της τυφλής οπής η μορφοποίηση του σπειρώματος πραγματοποιείται στο μεγαλύτερο τμήμα της οπής, ωστόσο, ένα τμήμα παραμένει χωρίς σπείρωμα προκειμένου να υπάρχει χώρος για την τοποθέτηση του κοχλία. Στο Σχήμα 4.50 παρουσιάζονται διάφορα είδη οπών, σε τρεις όψεις, τομή (ή πρόοψη) κάτοψη και άνοψη. Στο αριστερό τμήμα του σχήματος φαίνονται δύο οπές, μία διαμπερής και μία τυφλή, σε τομή. Στην τελευταία, η οπή καταλήγει σε ένα τρίγωνο, το οποίο σχηματίζεται από τη μύτη του τρυπανιού και έχει γωνία ίση με 120°. Στη μέση, παρουσιάζονται οι ίδιες οπές, αλλά με σπείρωμα, ενώ στο αριστερό τμήμα οι δύο οπές με σπείρωμα, αλλά σε πρόοψη. Στην τυφλή οπή με σπείρωμα, το τέλος του σπειρώματος σχεδιάζεται με παχιά συνεχή γραμμή. Η διαγράμμιση τέμνει την λεπτή γραμμή και τερματίζει στην παχιά γραμμή της κορυφής του σπειρώματος. Η ένδειξη του σπειρώματος σε κάτοψη ακολουθεί τον κανόνα που προαναφέρθηκε, η κορυφή του σπειρώματος με παχιά συνεχή γραμμή ενώ η βάση του σπειρώματος με λεπτή συνεχή. Να σημειωθεί ότι η βάση του σπειρώματος παρουσιάζεται με έναν κύκλο σχεδιασμένο κατά τα ¾ και περιστραμμένο ελαφρώς, έτσι ώστε το ένα άκρο του να τέμνει εμφανώς την αξονική γραμμή. Σε περίπτωση που το σπείρωμα δε φαίνεται, τότε σχεδιάζονται με διακεκομμένη γραμμή τόσο η κορυφή όσο και η βάση του σπειρώματος.
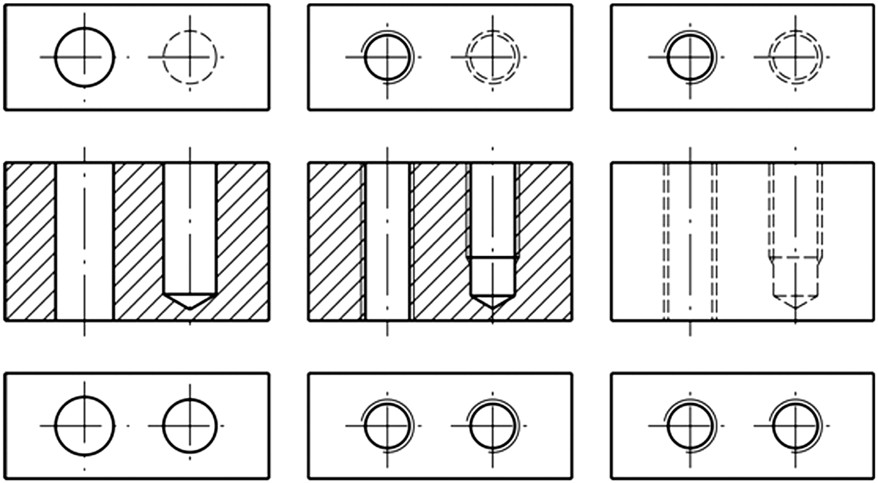
Σχήμα 4.50: Σχεδιασμός οπών με σπείρωμα.
Στους κοχλίες το σπείρωμα συμβολίζεται με τον ίδιο τρόπο όπως και στις οπές. Και σε αυτή την περίπτωση θα πρέπει να δοθεί προσοχή στη γραμμή τέλους του σπειρώματος, που σχεδιάζεται με παχιά συνεχή γραμμή (Σχήμα 4.51).

Σχήμα 4.51: Σχεδιασμός σπειρώματος σε κοχλίες.
Όπως έχει ήδη αναφερθεί οι κοχλίες χρησιμοποιούνται για την επίτευξη λυόμενων συνδέσεων. Στις περισσότερες περιπτώσεις οι κοχλίες συνδέουν δύο τεμάχια. Υπάρχουν δύο περιπτώσεις κοχλιοσυνδέσεων αναλόγως το τεμάχιο το οποίο φέρει σπείρωμα για το βίδωμα και το σφίξιμο του κοχλία. Στην πρώτη περίπτωση το τελευταίο τεμάχιο φέρει οπή με σπείρωμα, ενώ στη δεύτερη περίπτωση χρησιμοποιείται περικόχλιο. Στο Σχήμα 4.52 παρουσιάζονται οι πρώτη περίπτωση κοχλιοσύνδεσης. Σε αυτή την περίπτωση το πρώτο τεμάχιο φέρει διαμπερή οπή κατάλληλης διαμέτρου προκειμένου να περνάει ελεύθερα ο κοχλίας. Το δεύτερο τεμάχιο φέρει τυφλή οπή με σπείρωμα στο οποίο βιδώνεται ο κοχλίας.

Σχήμα 4.52: Σχεδιασμός κοχλιοσύνδεσης με κοχλία εξαγωνικής κεφαλής και τυφλή οπή με σπείρωμα.
Η δεύτερη περίπτωση κοχλιοσύνδεσης παρουσιάζεται στο Σχήμα 4.53. Τα δύο τεμάχια φέρουν διαμπερή οπή κατάλληλης διαμέτρου προκειμένου να περάσει ο κορμός του κοχλία. Η σύσφιξη πραγματοποιείται με τη χρήση περικοχλίου. Μεταξύ του δεύτερου τεμαχίου και του περικοχλίου τοποθετείται τυποποιημένη ροδέλα.

Σχήμα 4.53: Σχεδιασμός κοχλιοσύνδεσης με κοχλία εξαγωνικής κεφαλής και περικόχλιο.

Leave a Reply